スマホゲーム『魔王「世界の半分・・・:」』の周回の意味って
そのうちの1台はこまめに城を周回してアイテムをせっせと集めています。
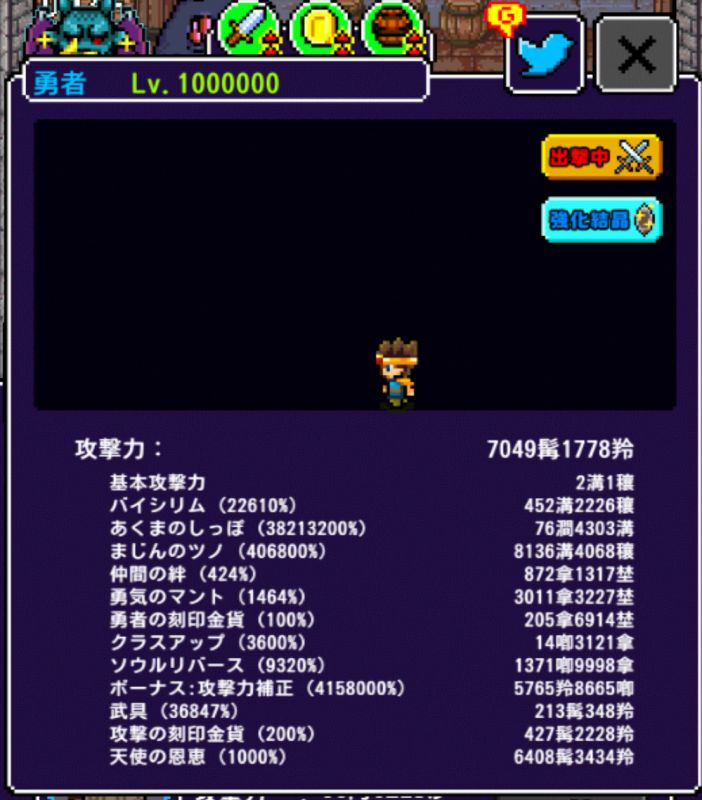
各パラメーターの勇者の攻撃力への影響と、周回の価値を検討してみました。
まず結論から
城を周回すると、わずかですがキャラクターの攻撃力が上がります。
これは「あくまのしっぽ」が攻撃力に影響しているためです。
ただし、その効果は直線的に増えるだけで、指数的に跳ね上がることはありません。
つまり、たくさん集めても「ほんの少しずつしか強くならない」という仕組みです。
実際に測定すると、約3400個集めてようやく基本攻撃力に匹敵する力が加わる計算になります。
しかし30万個も持っている状態では、1つ増えても攻撃力は0.000003倍しか伸びません。
これでは体感できないのも当然でしょう。
結論:ある程度以上集めても実質的な意味は薄く、周回は“自己満足”の領域になります。
とはいえ、ダイヤ回収のついでに周回するなら悪くはありません。
よくここまで集めました
長年の周回のおかげで「あくまのしっぽ」が30万個を超えるまでになっています。
標記攻撃力の計算式
①バイシリム攻撃力 =
基本攻撃力 x バイシリム% x 10000
②あくまのしっぽ攻撃力 =
基本攻撃力 x あくまのしっぽ% x10000
③まじんのツノ攻撃力 =
基本攻撃力 x まじんのツノ% x 10000
基本攻撃力は内部的にはその値を10000倍にして計算されているようです。それを考慮して、ここまでは表記の数字で計算できるのですが、「仲間の絆」からは突然単位が70桁も上がってきます。
「仲間の絆」なのでと、仲間の総攻撃力(仲間キャラクターの攻撃力を全て足し込んだ数値)を元に考えることにしました。
すると以下のような計算式が導き出されました。
④仲間の絆攻撃力 =
仲間の総攻撃力 x 仲間の絆%
⑤勇気のマント攻撃力
仲間の総攻撃力 x 勇気のマント%
⑥勇者の刻印金貨攻撃力 =
仲間の総攻撃力 x 者の刻印金貨%
⑦クラスアップ攻撃力で、⑥までのルールが適用できなくなりました。新たなルールを策定する必要があります。既存の攻撃力の合計(sum(①~⑥))という概念を取り入れることになります。
なお、①~③は無視しても誤差の範囲内です。
⑦クラスアップ攻撃力 =
sum(攻撃力①~⑥) x (クラスアップ% - 100%)
クラスアップ%から100% を減じる必要があります。(多分初期値に200%を与えて、クラスアップ0回なら100%として、条件分岐をなくす処理ですね)
⑧ソウルリバ ー ス攻撃力 =
sum(攻撃力①~⑦) x (ソウルリバ ー ス% - 100%)
なぜか、これもポ ー ナス:攻撃力補正%から100%を減じる必要があります。
⑨ポ ー ナス:攻撃力補正攻撃力 =
sum(攻撃力①~⑧) x (ポ ー ナス:攻撃力補正% - 100%)
これもポ ー ナス:攻撃力補正%から100%を減じる必要があります。
⑩武具攻撃力 =
sum(攻撃力①~⑨) x 武具攻撃力%
⑪攻撃の刻印金貨攻撃力 =
sum(攻撃力①~⑩) x 攻撃の刻印金貨%
⑫天使の恩恵 =
sum(攻撃力①~⑪) x 天使の恩恵%
攻撃力 =
sum(攻撃力①~⑫)で表されます。
実数字と計算式の検算の照合
計算結果は実数字と全て合致していることがおわかりいただけると思います。
| 達成度 | 表示攻撃力 | 計算 | |
| 攻撃力 | 7.0492E+223 | 7.0492E+223 | |
| 基本攻撃力 | 2.0001E+28 | ||
| ①バイシリム | 22610% | 4.5222E+34 | 4.5222E+34 |
| ②あくまのしっぽ | 38213200% | 7.6430E+37 | 7.6430E+37 |
| ③まじんのツノ | 406800% | 8.1364E+35 | 8.1364E+35 |
| ④仲間の絆 | 424% | 8.7213E+210 | 8.7215E+210 |
| ⑤勇気のマント | 1464% | 3.0113E+211 | 3.0114E+211 |
| ⑥勇者の刻印金貨 | 100% | 2.0569E+210 | 2.0570E+210 |
| ⑦クラスアップ | 3600% | 1.4312E+213 | 1.4312E+213 |
| ⑧ソウルリバ ー ス | 9320% | 1.3720E+215 | 1.3573E+215 |
| ⑨ポ ー ナス:攻撃力補正 | 4158000% | 5.7659E+219 | 5.7658E+219 |
| ⑩武具 | 36847% | 2.1303E+222 | 2.1304E+222 |
| ⑪攻撃の刻印金貨 | 200% | 4.2722E+222 | 4.2722E+222 |
| ⑫天使の恩恵 | 1000% | 6.4083E+223 | 6.4083E+223 |
| 仲間の総攻撃力 | 2.0570E+210 |
やり込んでいくと、「天使の恩恵」は1000%、「攻撃の刻印金貨」は200%と固定値になります。
そのため、最も影響を及ぼす要素は武具です。
任意の武具をレベル1上げると武具%は7%上昇しますが、すでに武具%が30,000に達している場合、
攻撃力の上昇はわずか0.02%にとどまります。
正直、やるせない気持ちになりますね。
2024年10月に実施(「従者の契約」が登場する前ですが、仲間の攻撃力には当該システムは影響ありませんので問題ないと考えます)
周回に対する疑問が...
ここで一つの疑問、つまりこのゲームをやり込んでいる者への警鐘が鳴り響きます。⑦の部分でも触れましたが、①~③は総合攻撃力を計算する上で、ほとんど誤差にもならない数値です。それを獲得するために一生懸命に周回しているなんて、無意味だと思いませんか?
でも、実際に周回は本当に無意味なのでしょうか?
「あくまのしっぽ」は多少影響あるみたいだけど
しばらく城を周回していると、微妙ながらも各キャラクターの攻撃力が上昇していることが確認できます。これは、周回によって獲得した「あくまのしっぽ」が②以外にも各キャラクターの攻撃力に影響を与えていることを示しています。ただし、「あくまのしっぽ」が具体的にどの程度攻撃力に影響を与えるのか、わざわざ周回する価値があるのかを考える必要があります。
そのため、その影響力を計測するために、数日間周回のみを行い、「あくまのしっぽ」とキャラクターの攻撃力の関係を調査しました。
前述のように、各要素は線形の関係にあるので、「あくまのしっぽ」一つ獲得するごとに一定の割合で攻撃力が増加するのでしょうか(推定式1)、それとも指数的な上昇を示すのでしょうか(推定式2)
Cf = Ar × An × Cb + Cb = (1+Ar) x Cb x An ・・・推定式1)
Cf = Cb × Ar^An・・・推定式2)
Cf:キャラクターの攻撃力、Ar:「あくまのしっぽ」1本当たりの上昇率、An:獲得した「あくまのしっぽ」総数、Cb:キャラクターの基本攻撃力(「あくまのしっぽ」を除いた総攻撃力)
いくらバブリーなゲームだからと言っても、推定式2)はまずあり得ないと思います。
実際に測定をして近似式を検討してみます。
「あくまのしっぽ」一つ当たりの上昇率を求める
あくまのしっぽを1759個集めました。すでに30万個以上を集めているので、この数は母数の0.5%程度に過ぎませんが、ここではその結果をもとに検討します。変化量の大きい最新のキャラクター、ハイエルフを例に挙げます。まず、最小二乗法による直線近似を行いました。
その結果、決定係数(R^2)は0.999842とほぼ1となり(下図)、推定式1)が妥当であることが証明されました。
|
あくまのしっぽ |
潜水士x 10200 | 軍曹x 10200 | ハイエルフx 10200 |
| 326183 | 1.5563 | 2.3057 | 5.8810 |
| 326255 | 1.5566 | 2.3062 | 5.8823 |
| 326518 | 1.5578 | 2.3081 | 5.8870 |
| 326777 | 1.5591 | 2.3099 | 5.8915 |
| 327942 | 1.5646 | 2.3180 | 5.9124 |
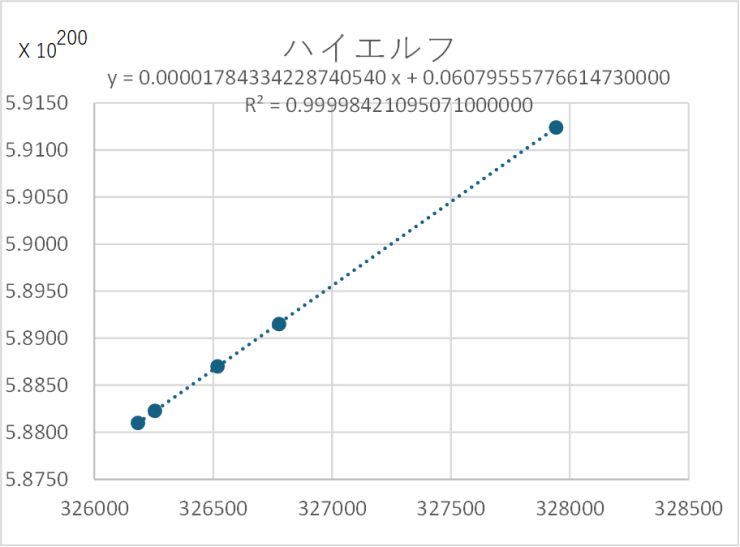
次にあくまのしっぽ1つ当たりの上昇率を検討します。推定式1)より、傾きは上昇率とCbの積で、Cbはy切片ですので、傾きをy切片(基本攻撃力)で除することで上昇率を求めることができます。計算すると、0.00001784334228731190 / 0.06079555775514310000 = 0.000293497
となり、その逆数は3407です。つまり、3400個のあくまのしっぽを集めると、キャラクターの基本攻撃力(「あくまのしっぽ」を除いた総攻撃力)に匹敵する力が加算されることになります。ただし、これは基本攻撃力に対する上昇率なので、大量にあくまのしっぽを保有する状態では、上昇の実感が薄れることがあります。
どの程度感じにくくなるかを実例をあげて以下に示します。A個のあくまのしっぽを保有している状態であくまのしっぽを1つ獲得した場合の攻撃力上昇率を表します。
(1+Ar) × Cb × (A+1) / (1+Ar) × Cb × A = (A + 1) / A = 1 + 1/A
すなわち、30万個のあくまのしっぽを集めた状態では、1つあくまのしっぽを獲得したところで攻撃力は1+1/30万=1.000003倍になったとしか実感できないということです。
実際、今回の検討でも1759個のあくまのしっぽを集めても、ハイエルフの攻撃力はこの計算通り5.8810 × 10^200から5.9124 × 10^200と、1.0053倍にしかなっていません。
これ以上あくまのしっぽを集める意味がないように感じられます。人それぞれの感覚には差があると思いますが、あくまのしっぽ集めのための周回は、ある程度以上は実質無意味です。
このゲームの数値表示は8桁で、おそらく内部計算は12桁まで行われていると思いますので、1兆個(10^12)まであくまのしっぽを集めてもカンストはされないでしょう。
まぁ、10分ごとに1回手に入るダイヤ回収のついでに周回しているから良しとしましょう。


